Many books have been written on communication in its widest sense. The interaction of people and their environment has been the subject of endless inquiry. The description of ideas and feelings in human relationships provides an infinite source of inspiration. However, the subject is often approached from the outside and deals with the manifestations of the process rather than the process itself. What actually happens when information exchanges? Why do people react in such and such way if they are faced with certain facts?
In the present approach – which is by no means the only way – a communication is seen as a process of interacting divisions. That means: any information exchange is translated into the sharing out of positions within a segmented reality. Two key words control, in my view, the process of communication: division and movement (fig. 4). These essential qualities will first be looked at in a provisional way to get acquainted with some of the mechanisms of data conveyance between people and environment.
Fig. 4 – Division (A) and movement (B) are the two major constituencies of any given communication (C). A. The dynamism of division leads to various sorts of measurements and subsequently to different types of visibility and B. The dynamism of movement plays an important role in the relation between the observer and the observed and is directly related to a definition of visibility.
The first variable (division) belongs to the foursome of basic arithmetical processes: adding, subtracting, multiplying and dividing. The second entity (movement) comes from a dualistic background, where static and dynamic natures are opposed to each other. Any preference of the usage of these subjects in a particular sequence is an arbitrary matter, but not without primary importance and significance.
Ernst BINDEL (1983) pointed to the present cultural preference of addition as the major arithmetical operation. There is no doubt, he said, that everything is geared towards addition: subtraction is just the opposite of it, multiplying is a continuous addition of the same units and division is the inversion of multiplication.
Counting and (digital) computing proved to be the best way to deal with the type of mechanical problems, which have been in the spotlight of our attention for a long time. And because they have worked so well in that particular area, they are gradually applied to a wider range of questions, including those of the human mind itself. Knowledge and thought became saturated with a world view based on the synthetic use of numbers, an addiction to addition.
Behind this preference lies the unwearied human need for the control of things. Everything should be included in our sphere of influence by listing the subjects one after another, like a Noah counting the animals when they were entering the Ark. That accumulation becomes a unity of knowledge and could manifest itself in power.
The ‘encyclopedic’’ movements in history provide instructive material with regards to the importance of addition in the consciousness of the people. The early medieval descriptions of nature, the sixteenth- and seventeenth century collectors, the French Encyclopaedeans and the modern computer-stored databases (like the Internet) have their devotion to addition in common. The celebration of quantities has a long history, which is closely related with a search for knowledge and power. The eternal dream that more is better has motivated generations of people and will continue to do so.
The importance of division is immanent from the outset of any communication, but not always visible in the classical sense of the word. It is only in the further course of communication, when motion is introduced, that the (primal) division provides the equipment to calculate the most crucial element in every communication: the visibility. This calculation – regardless of its nature – links the main components of a communication to a new unity (a value), which we call ‘visibility’.
The division is established in a cerebral process, which is part and parcel of the communication itself. The choice (following the numerical sequence 0, 1, 2, 3, 4, 5 … etc.) is made at the very moment a thought lingers on an object or subject. What is actually ‘seen’ in the mind of the observer is the product of a calculation.
Visibility can be expressed as a (numerical) figure derived from the shifting interaction of divisions.
The impulses produced in the process of seeing and thinking are stored in our brain. Visibility can be objectified as a code, consisting of a combination of numbers. This basic point of view will be elaborated on in a later stage of the investigation. For the time being, it will be sufficient to note, that the arrangement of numbers is highly dependent on the division which was used to store the information in the first place.
The ‘new’ subjectivity, which is proposed here, deals with a conscious notion of the principle of division. It is not the sort of negative subjectivity as indicated by Bertrand RUSSELL (1945, p. XXI) in the introduction of his classic ‘A History of Western Philosophy’: ‘Subjectivity, once let loose, could not be confined within limits until it had run its course’. Instead, it confines the human choices to clearly stated areas. If this is granted, the ominous anarchism is just a pioneering excursion of the mind to the borders of its own choice.
The coding pattern, derived from signals, together with that other, ever-growing reservoir of structured information, which is called memory (as an array of signals), makes up the stuff we think we are: a pattern of configurations, placed in time and based on a certain type of division. The storage of impressions, actions and relations in our mind is of the utmost importance to create our own visibility (identity). It explains why nobody is the same. The possibility to have access to a great variety of division models during our life, at different times and under diverse circumstances, gives an endless multitude of patterns. Nobody’s coding composition is ever the same, although certain congruences do occur in similar division choices. Understanding will be improved in the latter situation.
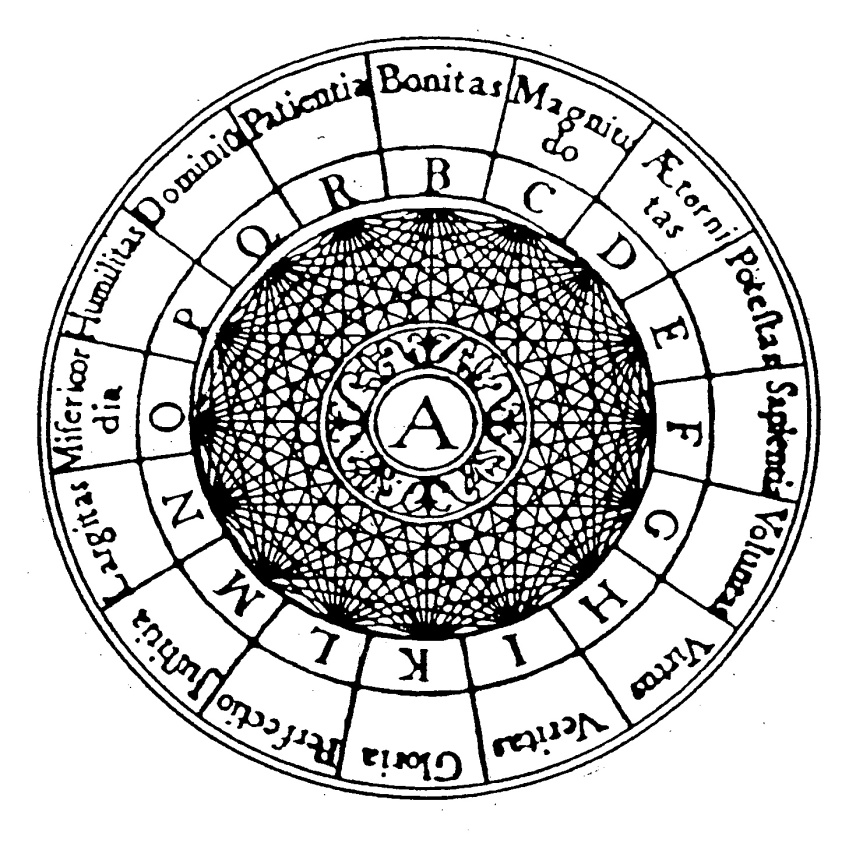
The idea that visibility – or in a wider sense: the employed stratagem to position our presence in a communication – could be calculated, is not new. It is the logic outcome of the understanding that visibility is a dynamic process, which is measurable. Long time ago the Catalan monk and scholar Raymond Lull (ca. 1232 – 1316) proposed a communication model based on revolving wheels. A particular combination of the wheels gave a sequence of letters, which had a certain meaning.
The Catalan monk and scholar Raymond Lull (ca. 1232 – 1316).
This elaborate system, known as his ‘Ars combinatoria’, was developed after he reached an illumination on Mount Randa, near the city of Palma de Majorca, in 1274. It was described some twenty years later in such books as the ‘Liber nova’ (1303), ‘Art generalis ultima’ (1308) and the ‘Ars brevis’ (1308). The latter book gave four basic figures to represent the relations between the primary (divine) principles: the A-figure, the T-figure, a table of relations and concentric wheels. All these figures tried to express certain dynamic properties of a communication in such a way that they are countable.
The main feature of the system was the employment of concentric circles, which were divided in ‘camerae’ (fig. 5). Each of these divisions was given a letter. A stood for God, B for goodness (bonitas), C for greatness (magnitudo), D for destiny (eternitas), etc. A total of sixteen divine attributes were distinguished. A new truth was created in a particular combination. Insight was, according to Lull, the outcome of a cyclic process and could be expressed in a simple basic principle.
Fig. 5 – The ‘figure A’, representing God, is the first to seven basic ‘figures’ in the Art of Ramon Lull. The sixteen compartments (or ‘camerae’) around the circumference contain letters from B – R (omitting J which was not used in Latin). They stand for the divine attributes. Each combination gives a truth about God.
A fresh impulse of enthusiasm for Lull’s ideas was given by Giordano Bruno, who edited in 1582 in Paris a book called ‘De Architectura Lulliana’ (De Compendiosa Architectura et Complemento Artis Lullii). This was a genuine effort to describe the dynamic system of Lull as faithful as possible. In 1587, he repeated his mission (in Wittenberg) with an edition of ‘De Lampade Combinatoria et de specierum scrutinio’, which gave a survey of the combinatorial possibilities of Lull’s system (TOCCO & VITELLI, 1890/facs. edition 1962).
The ‘Ars Lulliana’ had Bruno’s special interest because it fitted in his own inquisitiveness in the imagination and the character of knowledge. HENTSCHEL (1988) is opposed to Yates’ theses that Bruno was an ‘out-and-out magician’ and a ‘Hermetist of the deepest dye’ (HENTSCHEL, 1988; YATES, 1964; 1982) who established his hermetic philosophy for religious and political reasons. This criticism does not, in my opinion, full justice to Yates’ balanced view of Giordano Bruno’s position as an explorer of the intellectual world in the sixteenth century. Raymond Lull and Bruno, some three hundred years later, were searching for the same truth hidden in a universal communication model. This truthfulness did not tie in, for various reasons, with the power-obsessed ideas of the Roman Catholic Church in the period between 1200 and 1600.
The French philosopher and mathematician René Descartes (1596 – 1650) wrote in March 1619 to his friend Isaac Beeckman that his system of knowledge, based on analytical geometry, would be a replacement of the Art of Ramon Lull (KUBBINGA, 1989; ADAM & TANNERY (Ed.), 1908; Vol. X, pp. 156/157). This bold statement of Descartes was not far off the mark. The dualistic powers of Cartesianism became to rule the intellectual climate in Europe for a long time to come. Cyclic reasoning and its associated valuation methods were pushed to the background of the (scientific) stage in favor of a linear approach.
The German mathematician Gottfried Wilhelm von Leibniz (1646 – 1716) gave, at the apex of dualistic thinking, a new appraisal of the work of Lull. His ‘Dissertatio de arte combinatoria’ was submitted in 1666 at the University of Altdorf. The principle of division and the interaction of parts had been the major interest in Leibniz’ life. This interest led him to research every bit of uncharted territory, and he invented – simultaneously with Newton – the differential and integral calculus in 1675. He ventured, as one of the first, in the manufacturing of a calculating machine, which could not only add and subtract, but also multiply and divide – and even find the roots of numbers.
Leibniz traveled extensively on diplomatic missions and met the ‘natural philosophers’ Huygens, Malbranche and Arnaud (in Paris), Boyle and Oldenburg (in England) and van Leeuwenhoek and Spinoza (in Holland). The last part of his life was spent in relative obscurity as a librarian, preparing the history of the house of Brunswick. His opposition to the Newtonian cosmology of absolute matter, space and time resulted in the development of a theory based on the one division. He proposed, in his Monadology (1714), so-called monads as the foundation of all reality.
A major presentation of Lull’s work was accomplished by the teacher and printer Ivo Salzinger in Mainz (Germany). He published the ‘Opera omnia’ (Mainz edition) from 1721 – 1742 (YATES, 1954). Lull’s theory, in which he could ‘calculate from the fundamental patterns of nature an Art, which could be applied by analogy to all arts and sciences’ reached an apex of visibility.
The introduction of communication as a process of revolving wheels is, therefore, the continuation of a distinct historical line of thinking. Its main character is the ‘a priori’-departure that every piece of information, which is exchanged in the universe, is envisaged as the product of a contact between cyclic units. The full credit for the idea of revolving wheels must be given to Raymond Lull. None of the Greek philosophers or their Roman imitators had ever come up with such a view, although Empedocles might have been close to the target.
It was rather unfortunate that the mechanics of Lull’s Art were either misunderstood or misused in the ages to come. On top of that, it is unmistakable true that Lull himself contributed to the confusion, because he left little room for the interpretation of the combinatorial facts. He was also not clear on the nature of the initial division of his wheels. There are an eight or sixteen-division (A-, S- and X-figure), five- and fifteen divisions (T-figure) and a fourteen-division (figure V, seven virtues/vices). Furthermore, the number of concentric circles varied. Two or three circles were most common, but the figura universalis consisted of fourteen circles. The number of combinations of such a device is truly mind-boggling.
Lull can be credited to invent the mechanism of the combinatorial art and provide a practical way to calculate the intensio (approach) or remissio (alienation) between the communication partners. These terms, which were originally used by Scholastic philosophers in the thirteenth and fourteenth century to describe a change in quality (DIJKSTERHUIS, 1950/1986), are reintroduced here. They express, in a transparent way, the changes in intensity, which occur during an interchange of information. There is, for those with a historical conscience, a direct reminiscence to the oppositional forces of Love and Strife, which had long been recognized by Empedocles as the energy output of division thinking.
Partitioning is the most basic and authentic constituent of any reasoning. It brings any individual, who is interested in its nature, right in the middle of philosophy and theology. A part can be defined as a compartment of the universe, bounded by the markers of a division and subject to the laws of the universe. The two components of this definition, which are of equal importance, lead to all the problems related to delimitation and the application of rules. The part is the most important and integrated entity of a communication, and cannot escape its mutual bond.
This point was firmly taken by the ancient Greek, who regarded all gods as subordinate to a remote power called Destiny or Fate. The ultimate destiny that was called Moira. This name means ‘part’ or ‘allotted portion’ (CORNFORD, 1912; OTTO, 1954). The Greek historian Homer, living in the eight century BC, used the name, with one exception, always in an impersonal way. He described the gods, in the great epics of the Illias and Odyssee, as if they were human beings. All gods belonged to the earth, and had their share in life as in death. They mingled easily with the great heroes, like Agamemnon and Odysseus.
However, those heroic people also had their misfortunes orchestrated by Destiny or Moira (‘the Part’). They were, in other words, victims of the process of division, and, ultimately, of the whims of communication itself. Demeter’s daughter Persephone was robbed by Pluto while picking flowers and taken to the underworld to be become his wife. It was only after the intervention of the upper god Zeus, that Persephone was allowed one half-year with her mother on earth and the other half with Pluto in the underworld. The hero Ajax was drowned on his return from Troy. Orpheus was a singer, who was killed by Thracian women, because he withdrew himself from the community. Poor Tantalus, who offered his own son as food for the gods, was punished by having a perpetual hunger and thirst. And the wicked Sisyphus was condemned to push a rock up the hill, over and over again.
Many more gods had their human pleasures and pains, caused by the unpredictable nature of Moira. Her remote presence gradually turned from a spatial into a temporal concept. The single Moira (unity) became a threesome, the Three Daughters of Night. The three Fates portrayed a division in time: past, present and future. This plural aspect was first represented by Hesiod – where the three Moirai were daughters of Zeus and Themis – and came later to light in the Orphic theogony. The Fates were given as the children of Uranus and Gaia. The Cretan philosopher Epimenides (who once claimed that ‘all Cretans are liars’, and was credited as the author of the liar’s paradox) described Cronos and Eunyme as the parents of the Moirai, Aphrodite and the Erinyes. Later folk belief had lost all connections with an allotment or an area of primordial unity.